足し算引き算の途中や結果がマイナス、すなわち、負の値になる計算は、珠算2級以上の見取り算で要求されるスキルになります。
そろばんで負の値を扱う足し算引き算は、負の概念をしっかり理解できている方であれば、子供でも 大人でも簡単にマスターできる内容です。
[目次]
1.負の値を扱う足し算引き算概要
2.補数計算:そろばんの負の値を扱う足し算引き算
2.1.ステップ1:そろばんでは4桁くらい上の金額を借りる
2.2.そろばんの各桁の値
2.3.ステップ2:1の補数
2.4.ステップ3:2の補数
2.5.負の値に正の値を足したら正の値になるときもある
3.まとめ
1.負の値を扱う足し算引き算概要
例えば、A君がお財布に全財産の200円を入れて、おかあさんと一緒にコンビニにアイスクリームを買いに行ったとします。
ところが、A君の大好きなアイスクリームが値上がりしていて、243円になっていました。
お金が足りないので、A君はそばにいたおかあさんに足りない43円を借りました。
そして、無事アイスクリームを買うことができました。
…これがリアルな話での負の値を扱う足し算引き算です。
A君の財産は、43円の負債、すなわち、-43円です。
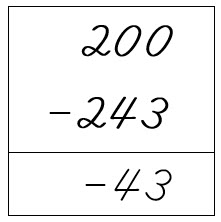
そろばんでは、この計算を次に説明する補数計算と呼ばれる3つのステップで行います。
2.補数計算:そろばんの負の値を扱う足し算引き算
先の例のように、アイスクリームなどを買うとき、足りない分をおかあさんに借りる場合は、足りない金額ちょうどを借りることが多いかもしれません。
一方、友達からお金を借りるときは、少ない額を貸し借りすると貸し借りした双方が貸し借りした事実を忘れるかもしれないということで、ちょっとまとまった額、例えば、この例の場合なら100円とか500円とか1000円くらいの額を借りるかもしれません。
2.1.ステップ1:そろばんでは4桁くらい上の金額を借りる
そろばんの計算でも、負の値になることがわかった引き算の時点で、引く直前に借金をします。
そろばんの計算でする借金は、おかあさんに借りるときのようなプラマイゼロになるような額ではなく、また、友達に借りるようなちょっと多めの切りのいい額でもなく、とてつもなく多めの切りのいい額を借ります。
具体的には、現在扱っている桁の4桁くらい上の桁の1で始まる額を借ります。
この話の例なら、3桁の計算をしている最中に負の値になることがわかったので、3桁のさらに4桁上の桁で1で始まる額、すなわち、1,000,000円借ります。
そして、1,000,200円から243円を引く計算をします。

この計算結果(例.999,957)のそろばんの盤面から読み取って、答え(例.-43)を導きます。
その読み取り方は、以下で説明します。
2.2.そろばんの各桁の値
そろばんは、上横一列にある五珠(ごだま)と、梁(はり)と呼ばれる横棒を挟んで、その下にある一珠(いちだま)で構成されています。
一珠1つで1の値、五珠1つで5の値を持っています。
ただし、一珠と五珠がそれぞれ1と5として値が有効になるのは、梁に直接、または、間接的にくっついているときだけです。
そろばんでは、縦にある5つの珠で、ある桁の数値を表現します。
例えば、一珠が2つと五珠が梁にくっついている桁の数は、7です。

2.3.ステップ2:1の補数
さて、負の計算結果を読むには、通常とは異なり、各桁の使っていない珠、すなわち、梁から離れている珠の合計を読み取ります。
読み取りはステップ2とステップ3で説明する2段階で行います。
各桁の使っていない珠の合計で表される数を1の補数と言います。
ステップ2では、1の補数を読みます。

例えば、999,957では、各桁の使っていない珠の合計000,042、要は、42が、1の補数です。
1の補数(例.42)は、それを元の数(例.999,957)に足すと、全部の桁が9になる値です。
2.4.ステップ3:2の補数
ステップ3では、1の補数に1を足した数である2の補数を求めます。
上記の例では、1の補数が42だったので、この2の補数は43となります。
この2の補数にマイナス記号を付けた数が、負の計算結果の値-43となります。
これには、理由があり、今そろばん上で求めた数999,957に43を足すと、1,000,000になり、借金をした1,000,000ちょうどになります。
2.5.負の値に正の値を足したら正の値になるときもある
例えば、A君からアイスクリームが値上げされていた話を聞いたおとうさんが、このあとA君に80円あげたとします。
そろばん上、999,957になっているところに80足すと、1,000,037になります。
これは、借りた1,000,000円を返せたことになり、この計算結果はプラス(正の数)の37です。
3.まとめ
そろばんの負の数の計算で、借金をするときに、現在の桁よりも4桁くらい大きい額を借りる理由は、次の2つです。
1.現在借金中であることが明確にわかる借り方をするため
2.途中でさらに大きな額を引かなければならなくなったときに、計算がわからなくならないようにするため
そろばんでは、見取り算でも読み上げ算でも、出題される問題の桁数の範囲が予め知らされているので、想定される最大の桁よりも3~4桁大きい桁に1を付けた額を借金して計算します。
補数の概念は、コンピューターなどでも利用されています。
これは、10進数だけでなく、2進数でも、8進数でも、16進数でも、同様に使われている方法です。
補数を使う計算なので、そろばんの負の数を扱う足し算引き算のことを補数計算と呼ぶこともあります。
この補数計算ができれば、珠算2級以上の見取り算の計算ができます。
結構簡単だったのではないでしょうか。

コメント