プログラミングの世界では、10進数はもとより、2進数や16進数を利用したり、2進数や16進数で考えたりすることがあります。
そこで、今回は、これらの進数の変換方法(今回は整数の範囲)を説明します。
高校の教科「情報」などで、すでに、学習した方は、復習としてご覧ください。
【目次】
1.N進法とは
1.1.底とは
1.2.N進法で使用する記号
1.3.N進法で数値を表す方法
1.4.N進数とは
1.5.N進数の表記方法
2.N進数を10進数に変換する方法
2.1.10進数の各桁の意味
2.2.2進数を10進数に変換する方法
2.3.16進数を10進数に変換する方法
3.10進数をN進数に変換する方法
3.1.10進数を10で割り続けてみると…
3.2.10進数を2進数に変換する方法
3.3.10進数を16進数に変換する方法
4.2進数と16進数の変換
4.1.16進数を2進数に変換する方法
4.2.2進数を16進数に変換する方法
5.まとめ
1. N進法とは
私たちが日ごろ数を数えるとき、10進法を使っているのは、ご存知のとおりです。
N進法とは、数値の表現に、N種類の記号だけを使用する方法で、記数法とも、位取り記数法とも言います(以降、この記事では、基本的に用語「N進法」を使用します)。
1.1.底とは
底が10である10進法が広く使用される理由は、ヒトが知能を持ち始めたときから、数えるときに身近にある、自分の手の指を利用したためだったのではないかと想像できます。
西欧諸国などでは、12を基準にした考え方があり、例えば、12個をまとめて1ダースとする数え方(1ダースは12、1グロスは12ダース、1グレートグロスは12グロス、…)があり、これはその基準である12を底とする12進法になっています。
ITの世界でよく使われるのは、10進法、2進法、16進法の3つです。
C言語の仲間のプログラミング言語(C++、C#など)や、UNIXの仲間のオペレーティングシステムなどでは、8進法もよく使われます。
この記事では、特に10進法、2進法、16進法の3つを取り上げて説明します。
1.2.N進法で使用する記号
例えば、底Nが10の10進法では、10種類の数字の記号(0, 1, 2, 3, 4, 5, 6, 7, 8, 9)だけを使います。
例えば、底Nが2の2進法では、2種類の数字の記号(0, 1)だけを使います。
例えば、底Nが16の16進法では、10種類の数字の記号と6種類の英字の記号(0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F)の計16種類の記号だけを使います。
1.3.N進法で数値を表す方法
N進法では、使える記号の数を超えた数値を表現するとき、桁(位取りとも言います)を増やして複数の記号で数値を表します。
1.4.N進数とは
N進法で表したある数値を、N進数と言います。
1.5.N進数の表記方法
・10進数の表記方法
10進数は、10進法で表した数値です。
例えば、10進数の3桁の数「126」は、次のいずれかで表記します。

3つ目の表記は、数値の前に10進数を表す「0d」(ゼロディー)を付けます。
「d」は10進数を意味するdecimalの頭文字です。
・2進数の表記方法
2進数は、2進法で表した数値です。
例えば、2進数の3桁の数「101」は、次のいずれかで表記します。
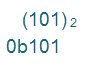
2つ目の表記は、数値の前に2進数を表す「0b」(ゼロビー)を付けます。
「b」は2進数を意味するbinaryの頭文字です。
・16進数の表記方法
16進数は、16進法で表した数値です。
例えば、16進数の3桁の数「3AC」は、次のいずれかで表記します。
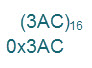
2つ目の表記は、数値の前に16進数を表す「0x」(ゼロエックス)を付けます。
「x」は16進数を意味するhexadecimalの3つ目の文字xを取ったものです。
なお、各進数の表記方法は、プログラミング言語やそれを利用する学校などのグループ内で、さらに独自の表記方法を使用する場合もあります。
2.N進数を10進数に変換する方法
2.1.10進数の各桁の意味
例えば、10進数の3桁の数126(0d126)は、数値が
126 = 1×(10の2乗) + 2×(10の1乗) + 6×(10の0乗)
であることを意味しています。
m桁から成る10進数は、各桁の記号(1桁分の数値)に、10の(桁目-1)乗を掛けて、それらをすべて足し合わせた値になります。
| m桁目の値 | ・・・ | 4桁目の値 | 3桁目の値 | 2桁目の値 | 1桁目の値 | |
|---|---|---|---|---|---|---|
| 上記に掛ける数 | ×10の(m-1)乗 | ×10の3乗= ×1000 | ×10の2乗= ×100 | ×10の1乗= ×10 | ×10の0乗= ×1 |
2進数も、16進数も、その他すべてのN進数も、上記の10進数の分解と同じ考え方を使って、10進数に変換することができます。
2.2.2進数を10進数に変換する方法
例えば、2進数の3桁の数101(0b101)は、10進数で
0b101 = 1×(2の2乗) + 0×(2の1乗) + 1×(2の0乗)
0b101 = 1×4 + 0×2 + 1×1
0b101 = 4 + 0 + 1
0b101 = 5
となります。
まとめると、m桁から成る2進数を10進数に変換するには、各桁の記号の数値(2進数の1桁分の数値、0か1)に、2の(桁目-1)乗を掛けて、それらをすべて足し合わせます。
| m桁目の値 | ・・・ | 4桁目の値 | 3桁目の値 | 2桁目の値 | 1桁目の値 | |
|---|---|---|---|---|---|---|
| 上記に掛ける数 | ×2の(m-1)乗 | ×2の3乗= ×8 | ×2の2乗= ×4 | ×2の1乗= ×2 | ×2の0乗= ×1 |
2.3.16進数を10進数に変換する方法
例えば、16進数の3桁の数3AC(0x3AC)は、10進数で
0x3AC = 3×(16の2乗) + A×(16の1乗) + C×(16の0乗)
0x3AC = 3×256 + 10×16 + 12×1
0x3AC = 768 + 160 + 12
0x3AC = 940
となります。
まとめると、m桁から成る16進数を10進数に変換するには、各桁の記号の数値(16進数の1桁分の10進数での数値、0~15の1つ)に、16の(桁目-1)乗を掛けて、それらをすべて足し合わせます。
| m桁目の値 | ・・・ | 4桁目の値 | 3桁目の値 | 2桁目の値 | 1桁目の値 | |
|---|---|---|---|---|---|---|
| 上記に掛ける数 | ×16の(m-1)乗 | ×16の3乗= ×4096 | ×16の2乗= ×256 | ×16の1乗= ×16 | ×16の0乗= ×1 |
3.10進数をN進数に変換する方法
3.1.10進数を10で割り続けてみると…
10進数の3桁の数値126(0d126)を10で割り続けてみると、次のようになります。
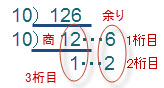
このように、10で割り続けると、1度目の割り算の余りは1桁目の数、2度目の割り算の余りは2桁目の数、これ以上10で割れなくなった数は、3桁目の数であることがわかります。
3.2.10進数を2進数に変換する方法
10進数を2進数に変換するには、10進数を2で割り続けます。
10進数の5(0d5)を2で割り続けてみると、次のようになります。
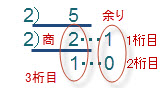
10進数を10で割り続けてみた結果と合わせて考えてみれば、2で割り続けると、1度目の割り算の余りは2進数の1桁目の数、2度目の割り算の余りは2桁目の数、これ以上2で割れなくなった数は、3桁目の数となります。
よって、10進数の5(0d5)を2進数で表すと0b101となります。
3.3.10進数を16進数に変換する方法
10進数を16進数に変換するには、10進数を16で割り続けます。
10進数940(0d940)を16で割り続けてみると、次のようになります。
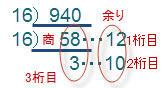
10進数を10で割り続けてみた結果と合わせて考えてみれば、16で割り続けると、1度目の割り算の余りは16進数の1桁目の数、2度目の割り算の余りは2桁目の数、これ以上16で割れなくなった数は、3桁目の数となります。
さらに、10進数の12は16進数ではC、10進数の10は16進数ではAなので、よって、10進数の940(0d940)を16進数で表すと0x3ACとなります。
・10進数をN進数に変換する方法
10進数をN進数に変換するには、10進数をNで割り続けます。
1回目の割り算で出た余りから順に、N進数の1桁目、2桁目…の記号(数字)となります。
4.2進数と16進数の変換
2進数と16進数は、簡単に相互に変換することができます。
まず、以下の、10進数で0~15を2進数と16進数でもそれぞれ表した表を、ご覧ください。
| 10進数 | 2進数 | 2進数(4桁になるよう0を挿入表示) | 16進数 |
|---|---|---|---|
| 0 | 0b0 | 0b0000 | 0x0 |
| 1 | 0b1 | 0b0001 | 0x1 |
| 2 | 0b10 | 0b0010 | 0x2 |
| 3 | 0b11 | 0b0011 | 0x3 |
| 4 | 0b100 | 0b0100 | 0x4 |
| 5 | 0b101 | 0b0101 | 0x5 |
| 6 | 0b110 | 0b0110 | 0x6 |
| 7 | 0b111 | 0b0111 | 0x7 |
| 8 | 0b1000 | 0b1000 | 0x8 |
| 9 | 0b1001 | 0b1001 | 0x9 |
| 10 | 0b1010 | 0b1010 | 0xA |
| 11 | 0b1011 | 0b1011 | 0xB |
| 12 | 0b1100 | 0b1100 | 0xC |
| 13 | 0b1101 | 0b1101 | 0xD |
| 14 | 0b1110 | 0b1110 | 0xE |
| 15 | 0b1111 | 0b1111 | 0xF |
表1.0~15の表記の比較:10進数、2進数、16進数
この表1を見て分かるように、16進数の1桁分の数値は、2進数の4桁分と対応します。
これは、16が2の4乗であるためです。
4.1.16進数を2進数に変換する方法
ある16進数を2進数に変換する方法は、基本的には、その16進数の各桁の数を、表1の対応する4桁の2進数で置き換えるだけです。
例えば、16進数の0x3ACを2進数に変換するには、表1より、
16進数の1桁目のC→4桁の2進数の1100(新しく作る1桁目から4桁目)
16進数の2桁目のA→4桁の2進数の1010(新しく作る5桁目から8桁目)
16進数の3桁目の3→4桁の2進数の0011(新しく作る9桁目から12桁目)
なので0b001110101100となりますが、特別な場合を除き、通常では(0bの直後の)先頭から続くゼロはすべて書かないので、よって、16進数の0x3ACは、2進数に変換すると0b1110101100となります。
4.2.2進数を16進数に変換する方法
ある2進数を16進数に変換する方法は、基本的には、その2進数の1桁目から4桁分ごとに、表1の対応する16進数の数で置き換えるだけです。
例えば、2進数の0b1110101100を16進数に変換するには、上記表より、
2進数の1桁目から4桁目 1100 →16進数のC
2進数の5桁目から8桁目 1010 →16進数のA
2進数の9桁目から10桁目 11→16進数の3
なので0x3ACとなります。
5.まとめ
プログラミングにおいて、N進法の変換に関する知識は、色を作るときなどに、必要になります。
今後、N進法の変換に関する知識が必要になったときも、知識を確認し定着させるために、再度こちらの記事をご覧いただくことをお勧めします。

コメント